
Fairly general, even discontinuous, periodic functions can be written as an infinite series in sines and cosines:
Such expansions are called Fourier series. If the y-axis lies halfway bewteen two of the discontinuities in the sawtooth, a formula for the sawtooth wave is something like
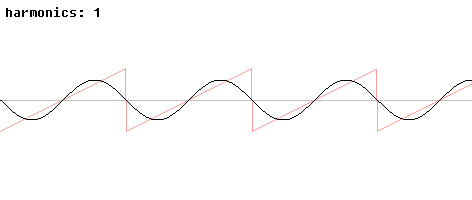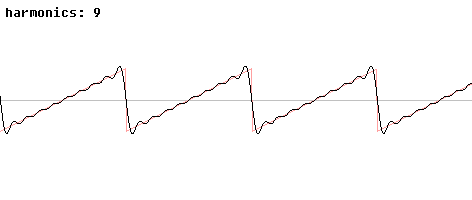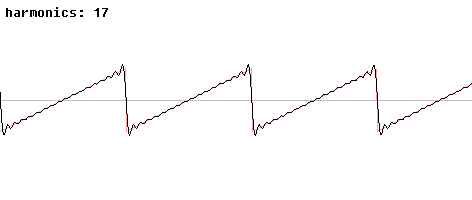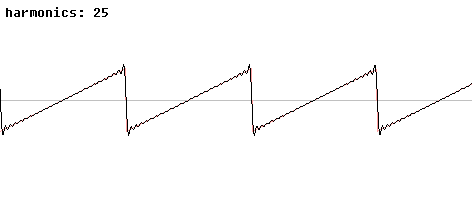
Below are two pictures of a periodic sawtooth wave and the approximations to it using the initial terms of its Fourier series.


The undershooting and overshooting of the finite series near the discontinuities is called the Gibbs phenomenon. It disappears in the full series but is present in every finite approximation, so it is an important issue to handle in signal processing. To hear the finite approximations to a sawtooth wave, look here.